What is abstract maths?
What is abstract maths and why is it so complicated? It’s a question many students will ask while grappling with a particularly complex calculus problem – and their teachers will probably echo while setting or marking tests.
It wasn’t always this way. Many fields of mathematics germinated from the study of real world problems, before the underlying rules and concepts were identified. These rules and concepts were then defined as abstract structures. For instance, algebra, the part of mathematics in which letters and other general symbols are used to represent numbers and quantities in formulas and equations was born from solving problems in arithmetic. Geometry emerged as people worked to solve problems dealing with distances and area in the real world.
What is "abstraction" in maths?
That process of moving from the concrete to the abstract scenario is known, appropriately enough, as abstraction. Through abstraction, the underlying essence of a mathematical concept can be extracted. People no longer have to depend on real world objects, as was once the case, to solve a mathematical puzzle. They can now generalise to have wider applications or by matching it to other structures can illuminate similar phenomena. An example is the adding of integers, fractions, complex numbers, vectors and matrices. The concept is the same, but the applications are different.
This evolution was necessary for the development of mathematics, and important for other scientific disciplines too.
Why is this important? Because the growth of abstraction in maths gave disciplines like chemistry, physics, astronomy, geology, meteorology the ability to explain a wide variety of complex physical phenomena that occur in nature. If you grasp the process of abstraction in mathematics, it will equip you to better understand abstraction occurring in other tough science subjects like chemistry or physics.
When do you use abstract maths?
The earliest example of abstraction was when humans counted before symbols existed. A sheep herder, for instance, needed to keep track of his flock of sheep without having any sort of symbolic system akin to numbers. So how did he do this to ensure that none of his sheep wandered away or got stolen?
One solution is to obtain a big supply of stones. He then moved the sheep one-by-one into an enclosed area. Each time a sheep passed, he placed a stone in a pile. Once all the sheep had passed, he got rid of the extra stones and was left with a pile of stones representing his flock.
Every time he needed to count the sheep, he removed the stones from his pile; one for each sheep. If he had stones left over, it means some sheep had wandered away or perhaps been stolen. This one-to-one correspondence helped the shepherd to keep track of his flock.
Today, we use the Arabic numbers (also known as the Hindu-Arabic numerals) to represent any integer, that is any whole number.
The Hindu-Arabic numerals are a set of 10 symbols—1, 2, 3, 4, 5, 6, 7, 8, 9, 0—that represent numbers in the decimal number system. They originated in India in the 6th or 7th century and were introduced to Europe through the writings of Middle Eastern mathematicians, especially al-Khwarizmi and al-Kindi, about the 12th century. They represented a profound break with previous methods of counting, such as the abacus, and paved the way for the development of algebra.
This is another example of abstraction, and it’s powerful. It means we’re able to handle any amount of sheep, regardless of how many stones we have. We’ve moved from real-world objects – stones, sheep – to the abstract. There is real strength in this: we’ve created a space where the rules are minimalistic, yet the games that can be played are endless.
Another advantage of abstraction is that it reveals a deeper connection between different fields of mathematics. Results in one field can suggest concepts and ideas to be explored in a related field. Occasionally, methods and techniques developed in one field can be directly applied to another field to create similar results.
Why is abstract maths hard?
Of course, abstraction also has its disadvantages. Some of the mathematical subjects taught at university level – Calculus, Real Analysis, Linear Algebra, Topology, Category Theory, Functional Analysis and Set Theory among them – are very advanced examples of abstraction.
These concepts can be quite difficult to learn. They’re often tough to visualise and their rules rather unintuitive to manipulate or reason with. This means students need a degree of mathematical maturity to process the shift from the concrete to the abstract.
Many high school kids come to university with an undeveloped level of intellectual maturity to handle abstraction. This is because of the way mathematics was taught at high school. I have seen many students struggling, giving up or not even attempting to study mathematics because they weren’t given the right tools at school level and they think that they just “can’t do maths”.
What's the best way to teach abstract maths?
In order to teach effective abstract maths, you need to teach your student the foundational concepts and make sure they understand what numbers are, and how to use them first.
Most student often struggle with Place Value, and this lack of understanding continues through primary and high school levels. Why is Place Value so hard? It's one of the most basic concepts in maths and MUST be mastered before moving on.
However, most often, teachers struggle with ways to explain Place Value and this step is often skipped.
What does Place Value have to do with abstract maths?
Place Value is simply "the value of a certain number in a particular place."
What is the place value of 1 in the hundreds column? It's "place value" is 100.
What if the 1 was in the tens column? It's "place value" would then be 10.
And what if it was in the units column? It would be 1 unit.
You can see very quickly that if a student does not understand place value, they won't go very far with maths. They will start to struggle and end up hating the subject, saying "they're not a maths person."
But it's not maths that is the problem, it's the way it has been taught. What is Place Value was taught with hands-on blocks and the student could see, touch and feel the numbers and where they go?
Look at this simple example, as taught in the Math-U-See program:

Therefore, when the student understands that "each number has a place" and can identify the value of that place, they can then advance to addition and subtraction.
Why is Place Value so important?
You can't add numbers if you don't know where they go!
Think of this. Add 34 + 29.
What answer do you get? Is the correct answer 63 or 36? Or is it 6 + 3 = 9?
See, you would know that if you understood place value properly.
If your student has understood and mastered this topic, the rest is easy. They can move forward to addition, subtraction, multiplication and even algebra.
You can watch the demonstration of how we teach Place Value to students here:
After learning Place Value, what next?
The key to learning maths is through multisensory methods and specific tools that support hands-on, tactile learning.
You can see that with Place Value - as soon as you have the hands-on manipulatives, the concept becomes easy to teach and even easier for the student to understand. Why? Because they can use their senses to engage with the numbers, not just the abstract squiggles on a page.
Therefore, we need to make sure that the hands-on tools are continued through the student's maths instruction to create strong foundations. Not just for Place Value. But for every topic all the way to algebra, geometry and beyond. Laying strong foundations will serve your students well before they start learning abstract maths.
What is Concrete-Representational-Abstract (CRA) methodology?
As explained above, we need the hands-on tools to teach maths effectively. That's where this methodology comes in. It's a research-proven way of teaching any subject - especially maths. Because of the complex nature of numbers and the fact they are often taught beginning with an abstract method, it doesn't work.
That's why we've created an entire program and step-by-step instructions to teach maths - with the hands-on tools and the proper methodology. The Math-U-See program has been used for parents, teachers and schools across Australia and internationally and has huge success with teaching maths, from foundational maths to abstract maths.
Here's what the CRA methodology looks like:
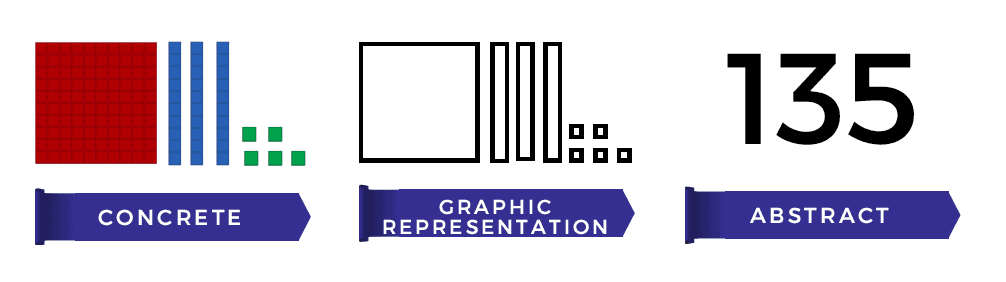
You can use this simple methodology to teach your student with the hands-on, tactile manipulatives (concrete phase) and ask them to draw the pictures of what that number looks like (the representational phase) before moving to writing down the number itself (the abstract phase).
Following this procedure is guaranteed to have better maths results. In fact, you'll have happy, confident students who engage in class and can use maths confidently in everyday life.
That's the final goal, huh? To have our students learn what we can teach them and be able to use it in their life (not just a meaningless subject at school that they hated and got poor results on an exam). We, as parents and teachers, want to be able to impact their world in a positive way and pave the way for successful study, career and employment opportunities.
It all starts with the foundations. And teaching those foundations properly before moving onto more complex abstract maths.
The answer is simple.
Use the hands-on manipulatives. For all maths instruction.
Your students will thank you later.
Want to get started?
The first place to start is to determine your student's current level of maths understanding. Have they conquered Place Value? Do they know addition and subtraction without finger counting? Can they easily multiply and divide?
There's an easy way to answer all those questions. You can take our free diagnostic test with your student to determine what they know and what they don't know. It's all online and very accessible to students.
At the end of the Placement Test, your student's results are automatically calculated. You'll know where to start and how to fill in those gaps in their maths understanding.
Here's the link to the free diagnostic Placement Tests:


