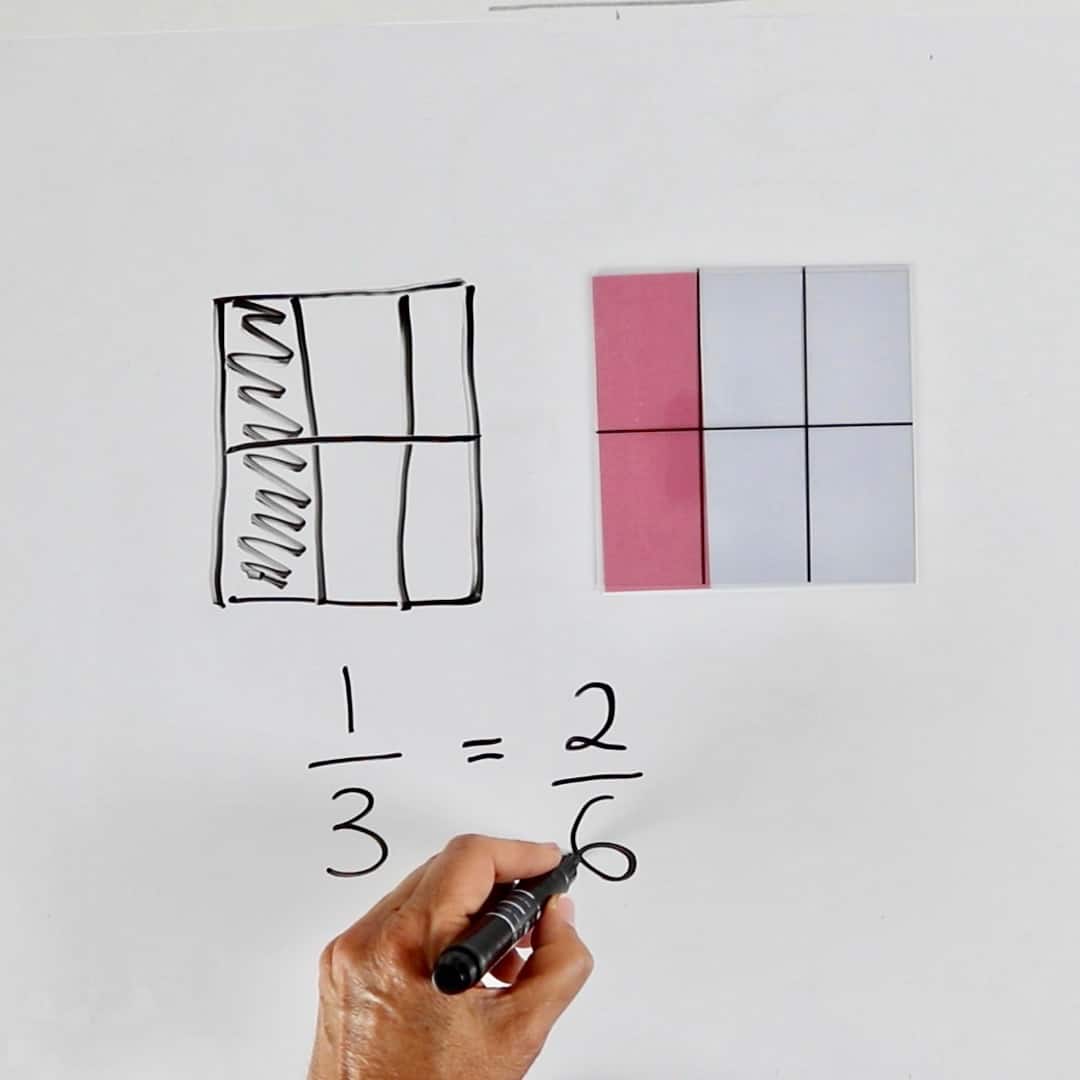
How to Teach Fractions in Maths

How to teach fractions in maths

There are so many ways to teach fractions in maths. Professors and teachers alike argue over which method is the best approach, and shudder when the results of fractions come back from student exams.

There's one key issue here to discuss. With all of the methods to teach fractions, online courses, tutorials and in-class presentations, there's one problem. None of the methods out there teach fractions in an accurate, truly hands-on way.

Why is that important? And is it even possible? Without using pizza and slices of fruit?
Yes. The first step with teaching any complex and more advanced maths topics is to make sure your student understands the foundational concepts first.

What does Place Value have to do with teaching fractions?

Does your student properly understand Place Value, basic addition and multiplication before moving onto fractions? This question is important because maths is a sequential subject. You need a strong foundation  to build upon - you need to ensure your student is not finger counting in Grade 6; that they have the understanding to be able to build on.

Fractions is especially hard to teach if your student doesn't first understand whole numbers and Place Value. It is a struggle to build on a shaky foundation, and your student will feel overwhelmed and want to give up. Perhaps, they just need a new approach? Perhaps your student is not "bad at maths" but has not beein taught in a way they understand. That's what I'm here to discuss today.

Before moving forward, you want to make sure you know where your student is at with maths. Here's a link to the free diagnostic test if you want to find out your student's current level of maths understanding. 

What are fractions and a "fraction of one"?

A "fraction" means a portion of something, a numerical quantity that is not a whole number (e.g. 1/2, 0.5) or a small or tiny part, amount, or proportion of something according to Wikipedia. It means you are asking for a piece of the pie, not the whole pie. 

When asking for a piece of the pie, you need to be able to show the student that the pie is still the same pie. It hasn't changed. It's still a blueberry pie. That's where most students get stuck. They think that the pie has changed flavours....or that when they are being taught fractions, that the number itself has changed. 

When finding a fraction of the pie, it's important to remember that the size of the pie hasn't changed. You're just asking for a smaller piece. 

Here's an example of 1/3 of one or "one whole, divided into three equal parts - and I want one of those parts."

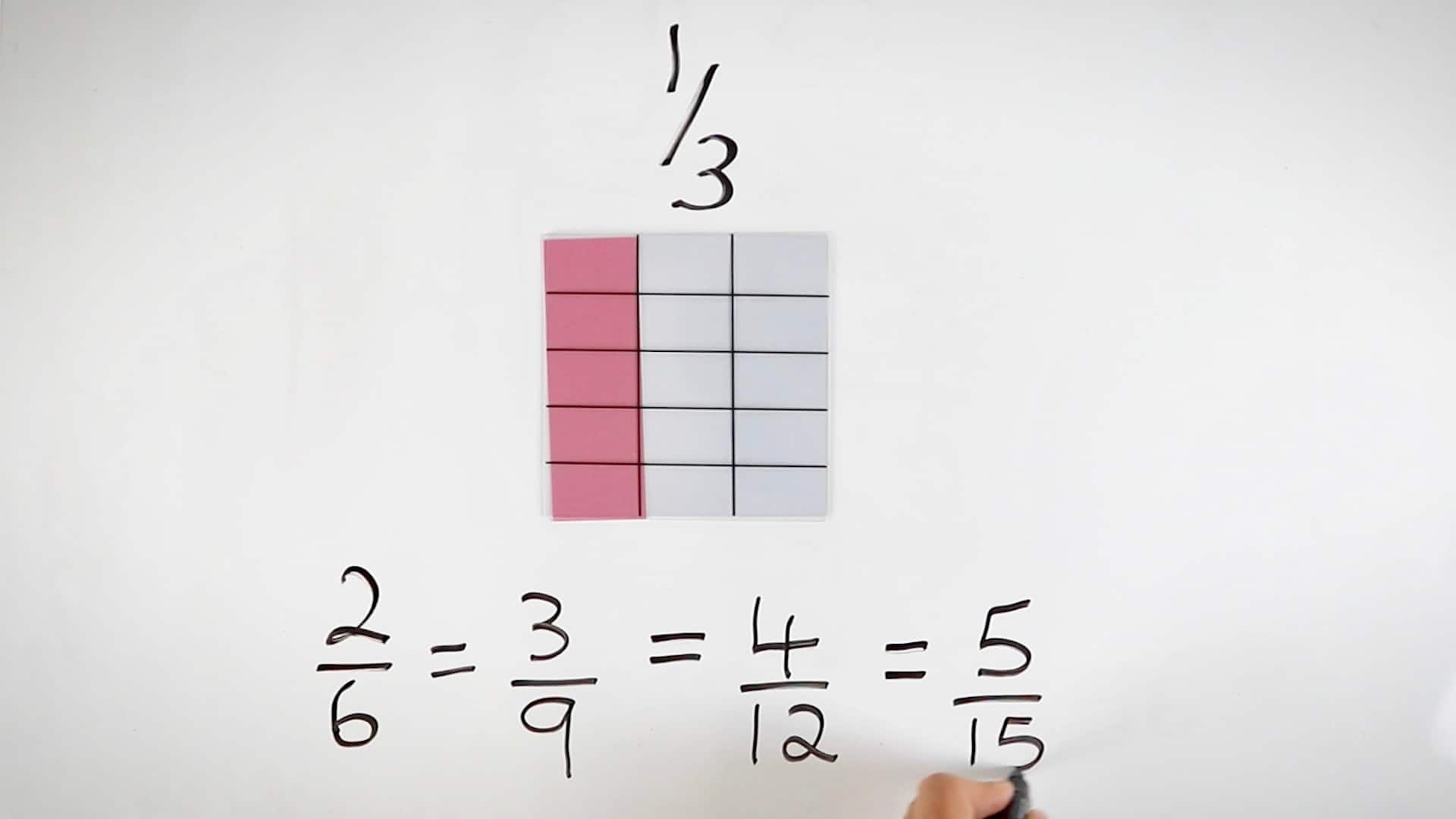
As you can see, with the coloured squares to represent the amount you want, it's simple to show your student equivalent fractions. 

By using the same pink colour as we do with whole numbers to show the number three, you help the student understand that you are still asking for a piece that is now divided into three equal parts -  or "one third" - even if the number of pieces expands. 

How to teach fractions, decimals and percents

We use the same methods to teach fractions, as we do decimals and percents.

When you think of it, a decimal is a fraction written in our linear, base ten system.... and a percent is a fraction written as 'per centime' or 'per one hundred'. Thus, we can expand the understanding of a fraction to decimals, percents and money. 

Here's an example of how we teach equivalent fractions and their relationship to decimals and percents:

You can see quite easily how fractions and a fraction of a number can convert into decimals, percents and money. We are talking about the same number and the same portion of a number.

Why use multisensory methods to teach maths?

We use this method of showing fractions, using the same colours from our Integer Block Kit to teach primary school to high school maths. By continuing to show numbers using the same colours all the way a child's schooling, they easily build on their knowledge - instead of trying to create a whole new system that just confuses them.

Here below are the hands-on, multisensory manipulatives we use for teaching addition, subtraction, multiplication, division and many other maths concepts:

Using these hands-on tools to teach numbers in the early years shows maths in a very simple and effective way. The abstract numbers on a page or written up on the whiteboard aren't just confusing squiggles anymore! They take on shape, colour and meaning for the student. 

The student can see that 9 is a light green colour with nine indents in the block and 3 is pink and has three indents. It's the same length as 10 + 2. 

Numbers become easy and simple to explain because you start working with the concrete before the abstract. By using research-proven CRA methodology, we teach students in a way that makes sense to them.

Here's what the CRA methodology looks like:

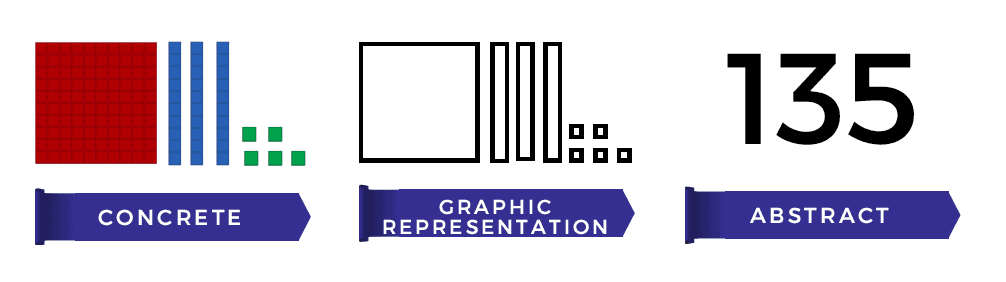
By starting with the concrete phase first, then going to the representational phase, and finally converting that understanding into the abstract numeral, the student gains a complete understanding of what's being taught. 

The same methodology is used for teaching fractions, decimals and percents and more advanced maths concepts. Using this proven methodology from a foundational level and continuing to more complex concepts, maths becomes much more engaging and students get better maths results!

What does research say about fractions and decimals?

It is always worth taking extra time to make sure your student understands and is mastering each concept before moving on, because without a solid foundation in the basics, students won’t be as able to succeed when they get to more advanced concepts.

A survey conducted by Roberg Siegler at Carnegie Mellon University appears to confirm that understanding basic math may have a significant impact on future learning.

The study shows that, while they may be similar in other ways (for example, similar grades in multiplication, or from similar family backgrounds), students who get poor grades in either fractions or division are more likely to get poor grades in algebra than students who got good grades in fractions and division.

“We suspected that early knowledge in these areas was absolutely crucial to later learning of more advanced mathematics, but did not have any evidence until now,” said Siegler, the Teresa Heinz Professor of Cognitive Psychology at CMU.

"The clear message is that we need to improve instruction in long division and fractions, which will require helping teachers to gain a deeper understanding of the concepts that underlie these mathematical operations. At present, many teachers lack this understanding. Because mastery of fractions, ratios, and proportions is necessary in a high percentage of contemporary occupations, we need to start making these improvements now." - Carnegie Mellon University

In a short video, Siegler explains more about the study and mentions that there have been several additional studies comparing teachers in the US and teachers in East Asia. The difference between the groups is their level of understanding. United States teachers are asked “Why is it a legitimate thing to invert and multiply when dividing fractions?” and can rarely give even one reason, while East Asian teachers can usually give two or three reasons why the procedures work that way. If the teacher doesn’t know why the formulas work, all the teacher can say is, “Just do it because it’s the right way to do it.” Unfortunately, both children and adults have difficulty remembering rote information that they don’t understand.

Equipping teachers and helping them and their students understand the concepts is essential. By valuing the understanding and mastery of each concept, students are supported to create strong foundations in maths to prepare them for advanced maths.

Looking for extra support to teach fractions?

To support you to confidently teach to your students fractions, decimals and percents in a multisensory way, we currently offer online and in-person Fractions, Decimals & Percents Training for teachers, tutors and intervention specialists. 

You can find out more about our upcoming Trainings here:

Let us know if you have any questions by contacting us directly here.

Looking forward to seeing you there!

Warmly,

The Team at Maths Australia