
Why does Australia have such devastating maths results?
Australian students are struggling with the way maths is being taught in schools and maths results are plummeting. They don't understand mathematical concepts, they struggle to understand Place Value and start hating maths. Bored students disrupt the class and others complain of being pushed too hard, and having too much pressure put on them.
When it comes time to exams, student results are shockingly poor. Teachers are pulling their hair out, trying to figure out what went wrong.
What's the solution?
We must first understand what students do, or do not, understand. There needs to be a clear snapshot of what has been integrated by the student before teaching any new concepts. Place Value, for example, is a basic foundational concept that is often misunderstood and even into high-school, students still can't understand the proper placement of numbers.
Secondly, students must be taught using effective tools. There is a massive gap in student understanding of maths because concepts are bing taught in an abstract manner with no concrete examples. By using specific hands-on manipulatives, the teacher creates a bridge between the concrete to the abstract and therefore creates a neurological bridge between the concept and memory, retention and how to use what they have been taught in the right context, giving students confidence with maths.
How do Australian students compare to those from other countries?
Australian students are notoriously bad at mathematics. Just look at the recent Trends in International Mathematics and Science study outlined in SMH 2016. Students are being taught concepts in class and then when the time comes for the test, they perform shockingly. They struggle to answer basic questions and understand what is being asked of them. They can't remember what they were taught.
Have a look at the Australian PISA maths results for 2018 (the most recent results to date). The OECD Programme for International Student Assessment (PISA) examines what students know in reading, mathematics and science, and what they can do with what they know. It provides the most comprehensive and rigorous international assessment of student learning outcomes to date.
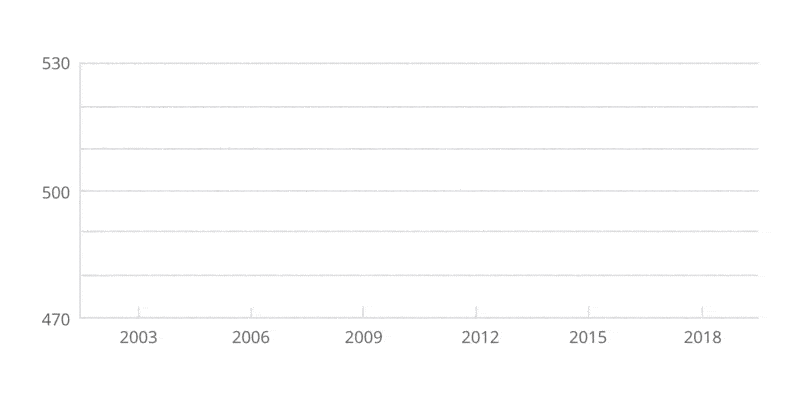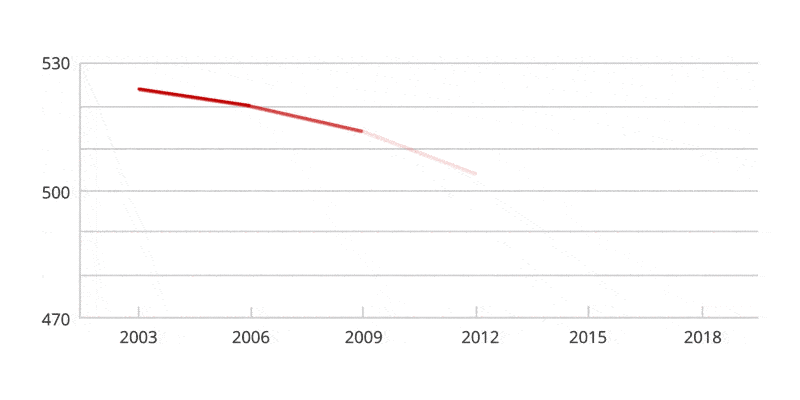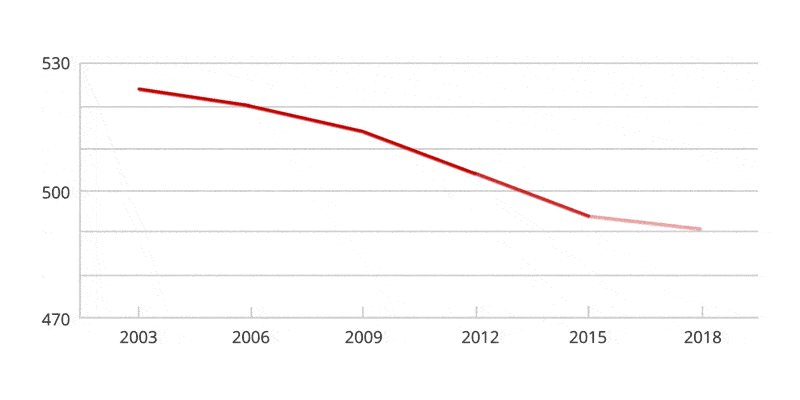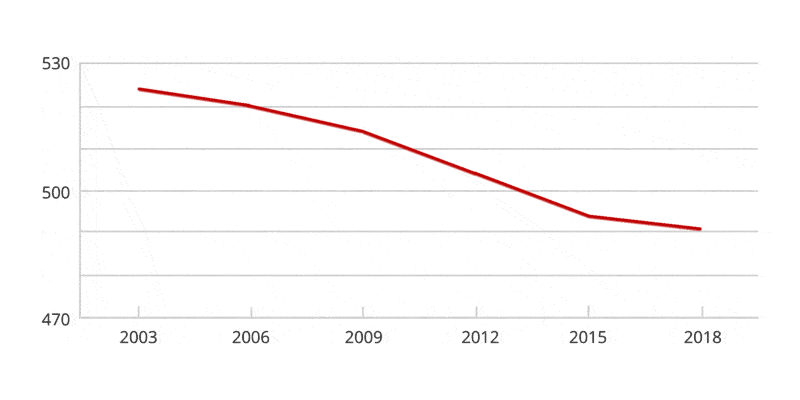
One of the main issues is that we don't teach our students the base-ten system. The first problem has to do with the names we give to our numbers. We say one, two, three, four, five, six, seven, eight, nine, ten—and then eleven, twelve. Why eleven and twelve? Those words provide no hint about the repeating nature of what is happening here. The numerals repeat, but the names do not. There’s nothing in these names that tells us explicitly that eleven is one added to ten and twelve is two added to ten. And then we go to thirteen, fourteen, etc. Even many adults don’t know that the teen here means ten, so thirteen is literally three and ten.
Contrast this to the maths languaging in Chinese, Japanese, and Korean. Those number names (translated literally into English), beginning with ten, go ten, ten one (for 11), ten two (for 12), etc., and then onto two-tens (for 20), two-tens one (for 21), and so on. The words repeat in exactly the way that the numerals repeat. For a child learning to count in any of these languages the base-ten system is completely transparent. It can’t be missed.
What are some important concepts that students need to learn?
There are some basic concepts that students must learn, in order to continue their understanding of maths. Through using grade levels as indicators of knowledge for a student, Professor Dianne Siemon shares her viewpoints on what is most crucial in a student's maths education.
Watch the video "Big Ideas in Numbers" below:
How does language relate to learning maths?
To understand how all this is relevant to learning arithmetic, consider a child learning to add two-digit numbers, say, 34 plus 12. English-speaking children pronounce the problem (aloud or to themselves) as “thirty-four plus twelve,” and the words provide no hint as to how to solve it. Chinese-speaking children, however, pronounce the problem (in effect) as “three-tens four plus ten two,” and the words themselves point to the solution. In the two numbers together there are four tens (three tens plus one ten) and six ones (four plus two), so the total is four-tens six (46).
One line of evidence that number words indeed do make a difference comes from a study showing that children in America learn to count to 10 at the same age, on average, as do Chinese children but fall behind Chinese children in learning to count beyond 10, which is where the languages begin to diverge (Miller et al., 1995). By age 4, most of the Chinese children studied could count to 40 or beyond, whereas most American children could not get past the low teens. These results are also seen in Australia.
Maths must be taught as a language. It needs to start with basic understanding using concrete examples and experiential knowledge, for students to be able to build on that understanding in a confident manner. The best test for student understanding of maths is using word problems. If a student can't apply what they have been taught in an everyday life situation, it is not a complete maths understanding. It was simply a formula learnt by rote, and therefore when the question doesn't match what they had rote memorised in class, they get the answer wrong.
What does the research say?
In an even more telling study, 6-year-olds in the United States, France and Sweden (where maths languaging contains irregularities) were compared with 6-year-olds in China, Japan, and Korea on a task that directly assessed their use of the base-10 system (Miura et al, 1994). All the children had recently begun first grade and had received no formal training in place value. Each was presented with a set of white and purple blocks and was told that the white blocks represent units (ones) and the purple blocks represent tens. To make it clear, the experimenter explained, “Ten of these white blocks are the same as one purple block,” and set out ten whites next to a purple to emphasize the equivalence. Each child was then asked to lay out a set of blocks to represent specific numbers—11, 13, 28, 30, and 42.
The results were striking. The Asian children made their task easier by using the purple blocks correctly on over 80 percent of the trials, but the American and European children did so on only about 10 percent. For example, while the typical Asian child set out four purples and two whites to represent 42, the typical American or European child laboriously counted out 42 whites (units). So, even before beginning any formal training in numerical calculations, the Asian children already have a head start—they implicitly know the base-ten system.
Why are base-ten numericals important?
The base-ten numerical system is a beautiful thing; it’s too bad we mess it up with our language and thereby hide its beauty from our children, and from ourselves too. That’s an effect of history and the power of tradition, which very frequently trump logic and aesthetics.
The number system that is used around the world—the decimal, or base-ten system—is built around a wonderfully simple pattern. There are ten numerals and they keep repeating, always in the same sequence. You begin with units at 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, and then, to go past 9, you put a 1 in the “tens place” and start over–10, 11, 12, 13, 14, 15, 16, 17, 18, 19—and then you put a 2 in the tens place …. and so on, and so on, and so on. Once you’ve got the system down you can do it forever if you like; you could spend your whole life at it and never come to the end.
The most crucial thing to understand if you want to do any calculations with this number system is its base-ten repeating nature. The algorithms that we teach children for adding, subtracting, multiplying and dividing are all necessarily founded on an understanding of place value and that pattern. If children don’t understand the base-ten pattern, they have no way of making sense of the procedures they are taught for calculating. They memorise the procedures without understanding, which means that they haven’t really learned them. They’re just going through motions, mechanically, without thought or reason. They take it on faith that the system works, because a teacher told them it does, only to come un-stuck when understanding is required and the teacher is not there.
This is why it's crucial to teach students using a sequential, step-by-step process, using hands-on tools and providing them the resources they need to be able to succeed in maths. We need to seriously look at our schooling system and fill in the gaps of teaching styles.
If you need to check your students understanding, to find out what they know and what they don't know, you can take the free diagnostic test here:
Let us know what your students are struggling with in the comments below,
Warmly,
The Team at Maths Australia
References:
[1] Portions of this post were taken from P. Gray, Psychology (6th edition, Worth Publishers).
[2] Miller, K. E., Smith, C. M., Zhu, J.,& Zhang, H. (1995). Preschool origins of cross-national differences in mathematical competence: The role of number-naming systems. Psychological Science, 6, 56-60.
[3] Miura, I. T., Okamoto, Y., Kim, C. C., Chang, C., Steere, M., & Fayol, M. (1994). Comparison of children’s cognitive representation of number: China, France, Japan, Korea, Sweden, and the United States. International Journal of Behavioral Development, 17, 401-411.

